Bappy's Blog

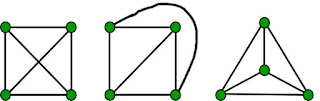
প্রথমেই জানা দরকার   Planar Graph  কী? Planar Graph হচ্ছে, দ্বিমাত্রিক তলে আঁকা এমন একটা গ্রাফ যেখানে একটা এজ কখনোই অন্য একটা এজকে ছেদ করবে না। একটি গ্রাফের Euler Characteristics বা Euler Number = Vertices - Edges + Faces এখানে, Faces = গ্রাফটির মোট সাইকেল + ১  এখানে, একটা সাইকেল কে তখনই হিসেবে আনবো যখন তার ভিতর অন্য কোন সাইকেল থাকবে না। মজার ব্যাপার হচ্ছে, Planar Graph এর জন্য সবসময় ই Euler Number = 2 ছবিতে, ১ম গ্রাফটি Planar Graph নয়! কারণ, একটা এজ অন্য এজ কে ছেদ করেছে। ২য় গ্রাফের জন্য, Euler Number = 4 - 6 + 4 = 2 ৩য় গ্রাফের জন্য, Euler Number = 4 - 6 +4 = 2 এভাবে, সকল Planar Graph এর জন্যই Euler Number = 2 যা অনেক থিওরিতে এপ্লাই করা লাগে। আশা করি, পরবর্তীতে কোন থিওরি তে এপ্লাই করে দেখাবো Planar Graph এর এই প্রোপার্টি। Happy Coding -_-

সমস্যাঃ  তোমাকে একটি দ্বিমাত্রিক তলের উপর অবস্থিত ২ টি বিন্দু দেয়া আছে। গ্রাফ পেপারে বিন্দু দুটি চিহ্নিত করে তাদের সংযোগ সরলরেখা আকলে ঐ সরলেখার উপর গ্রাফ পেপারের কয়টি বিন্দু পড়েছে সেটা বের করতে হবে। সমাধানঃ মনে করি, বিন্দুদ্বয় P(x1,y1) এবং Q(x2,y2) ।  ১) PQ সরলরেখা যদি X-অক্ষের সমান্তরাল হয় তবে ans = abs(x1 - x2) - 1 ২) PQ সরলরেখা যদি Y-অক্ষের সমান্তরাল হয় তবে ans = abs(y1 - y2) - 1 ৩) অন্যথায়, ans = GCD ( abs(y1-y2) , abs(x1-x2) )-1

Problem Description  here প্রব্লেমটিতে একটা সংখ্যা দেয়া থাকবে যার প্রাইম ফ্যাক্টরগুলো বের করতে বলা হয়েছে। সল্যুশন আইডিয়াঃ আমরা সাধারণত প্রাইম ফ্যাক্টরাইজ করি কীভাবে? প্রাইম জেনারেট করে স্কয়ার রুট পর্যন্ত প্রাইমগুলো দিয়ে কেটে কেটে! সেটার  (মানে আমি -_-) মূলত এই সোজা শাপটা প্রব্লেম দিয়েছে ই যাতে তোমার এই সল্যুশন TLE খায়! তাহলে উপায় কী! সবগুলো সংখ্যার ক্ষুদ্রতম প্রাইম ফ্যাক্টর বের করে নাও। যেমনঃ ৮ এর ক্ষুদ্রতম প্রাইম ফ্যাক্টর ২ , ১৫ এর ক্ষুদ্রতম প্রাইম ফ্যাক্টর ৩। মনে করো, আমি N = ৬০ এর প্রাইম ফ্যাক্টর বের করতে চাই। ৬০ পর্যন্ত সবার ক্ষুদ্রতম প্রাইম ফ্যাক্টর আমার অলরেডি জানা! Factor[] = { } step-1: SF[N] = 2 ; Add 2 to the list ; N = N/2 = 30 step-2: SF[N] = 2 ; Add 2 to the list ; N = N/2 = 15 step-3: SF[N] = 3 ; Add 3 to the list ; N = N/3 = 5 step-4: SF[N] = 5 ; Add 5 to the list ; N = N/5 = 1 Jump out from the loop!!! Now, Factor[] = { 2 , 2 , 3 , 5 } এখন, একটা সংখ্যার সর্বোচ্চ কয়টা প্রাইম ফ্যাক্টর থাকতে পারে? log(N) টা! তার মানে এক্সেক্ট log(N) বার লুপ ঘুর...