Light OJ - 1394 - Disable the Wand Tutorial
Problem Description here
এখন পর্যন্ত আমার সলভ করা ডিজিট ডিপির প্রব্লেমগুলোর মধ্যে অন্যতম মজার প্রব্লেম এই প্রব্লেমটি।
সংবিধিবদ্ধ সতর্কীকরণঃ এই পর্বের লিখা কিছুটা দীর্ঘায়িত হতে পারে। যা সম্পূর্ণ অনিচ্ছাকৃত । ডিজিট ডিপির ব্যাসিক আইডিয়া না জানলে এই পর্ব না পড়াই উত্তম। সেক্ষেত্রে, নিচের লিংক থেকে ব্যাসিক ডিজিট ডিপি শিখে আসা উচিৎ।
প্রব্লেমটিতে বলা হয়েছে, একটা রেঞ্জ এর মধ্যে যেসব সংখ্যা ৩ দ্বারা বিভাজ্য কিন্তু ৭ দ্বারা বিভাজ্য নয় এবং যাদের বাইনারী রিপ্রেজেন্টেশনে সর্বোচ্চ Maxone সংখ্যক 1 থাকতে পারে এবং একটি আইডিয়াল নাম্বার এর সাথে বিট ডিফারেন্স সর্বোচ্চ k হতে পারে তাদের যোগফল বের করতে।
২য় টেস্টকেস টা যদি দেখিঃ
1 6 2 3 2
1 থেকে 6 পর্যন্ত সংখ্যাগুলোর বাইনারী রিপ্রেজেন্টেশন হচ্ছেঃ
1 - 00000000000000000000000000000001
2 - 00000000000000000000000000000010
3 - 00000000000000000000000000000011
4 - 00000000000000000000000000000100
5 - 00000000000000000000000000000101
6 - 00000000000000000000000000000110
আইডিয়াল নাম্বার ৩ এর বাইনারী হচ্ছেঃ 00000000000000000000000000000011
1 এর সাথে আইডিয়াল নাম্বার এর কয়টা বিট মিলে না? ১ টা
2 এর সাথে আইডিয়াল নাম্বার এর কয়টা বিট মিলে না? ১ টা
3 এর সাথে আইডিয়াল নাম্বার এর কয়টা বিট মিলে না? ০ টা
4 এর সাথে আইডিয়াল নাম্বার এর কয়টা বিট মিলে না? ৩ টা
5 এর সাথে আইডিয়াল নাম্বার এর কয়টা বিট মিলে না? ২ টা
6 এর সাথে আইডিয়াল নাম্বার এর কয়টা বিট মিলে না? ২ টা
তার মানে রেঞ্জ এর মধ্যে যেসব সংখ্যা শর্তগুলো পূরণ করে তারা হলো ৩ এবং ৬।
সল্যুশন আইডিয়াঃ
মোটামুটি বোঝাই যাচ্ছে যে, এই প্রব্লেমে আমরা সংখ্যার বাইনারী রিপ্রেজেন্টেশন নিয়ে কাজ করা সহজ হবে।
প্রথমে আমি ১ থেকে end পর্যন্ত রেঞ্জে শর্তপূরণ করে এমন সংখ্যার যোগফল বের করবো।
এরপর আমি ১ থেকে start-1 পর্যন্ত রেঞ্জে শর্তপূরণ করে এমন সংখ্যার যোগফল বের করবো। আর বিয়োগ করে আউটপুট বের করবো।
যেসব স্টেট নিতে হবেঃ
State-1: Is the current number already became smaller than upper bound of the range?
State-2: Position
State-3: Total number of 1's used so far.
State-4: Bit differ from ideal number.
State-5: Value after mod by 3
State-6: Value after mod by 7
যেহেতু, লিমিট ১০^৯ তাই এই প্রব্লেমে আমি ৩০ টা বিট নিয়ে কাজ করেছি। মনে কর,
1 18 5 18 5
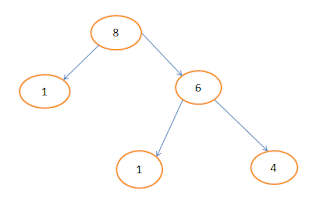
এই ইনপুটের জন্য আমি এখন ২৭ তম পজিশনে আছি।( পজিশন শুরু হয় ০ থেকে এবং ০ তম বিট হচ্ছে MSB) । তার মানে ২৭ তম পজিশনে বিট 1 বসালে ভ্যালু কত যোগ হয়? 1<<(30-27) = 8। আর এই 8 থেকে পরবর্তীতে আরো কোন কোন দিকে যায় তা আমি একটা ট্রি এর মতো করে দেখাবো।
উপরোক্ত ট্রি থেকে কী দেখা যাচ্ছে? ৮ থেকে ৩ টা ভ্যালিড পাথে যাওয়া সম্ভব। তার মানে, রেজাল্ট এর সাথে ৮ তিনবার যোগ হবে, গতানুগতিক প্রব্লেমের মতো একবার নয়! এই প্রব্লেম সলভ করার সময় আমি সবচেয়ে বেশি ডিফিকাল্টি ফেইস করছি এই জায়গাটা অবজার্ব করতে!
এখন, কথা হচ্ছে বর্তমান পজিশনে অর্থাৎ ৮ এ দাঁড়িয়ে আমি কিভাবে বলবো যে ৮ থেকে কয়টা ভ্যালিড পাথে যাওয়া সম্ভব? এজন্য, এই প্রব্লেমে মেমোরাইজেশন করার জন্য আমরা পেয়ার এর অ্যারে ব্যাবহার করবো। যার, প্রথম এলিমেন্টে আমি বর্তমান স্টেট থেকে সামনের দিকের সংখ্যাগুলোর যোগফল রাখবো। দ্বিতীয় এলিমেন্টে রাখবো, সামনের দিকের স্টেটে সর্বমোট কয়টা ভ্যালিড পাথে যাওয়া যায়।
এখন, আমি বর্তমান পজিশনের ভ্যালুর জন্য সামনের স্টেটের রিকার্শন কল করলেই জানতে পারি যে কয়টা পাথে যেতে পারবো বর্তমান পজিশনের ভ্যালু টা নিয়ে! তাহলে তো কাজ শেষ।
এই প্রব্লেমের বেস কেস কি হবে তাহলে?
যদি প্রব্লেমের শর্তাবলী পূরণ হয় তবে {0 , 1} নাহয় {0 , 0} রিটার্ণ করবো।
এবার প্রব্লেমটা নিজে নিজে করার চেষ্টা করা উচিৎ। কারণ, এই প্রব্লেম থেকে সত্যি অনেক কিছু শিখার আছে। তাও, না পারলে সল্যুশন দেখতে পারো নিজ দায়িত্বে।
............
Comments
Post a Comment