SPOJ - PARSUMS - Nonnegative Partial Sums with Sliding Range Minimum Query
See the problem description - Here
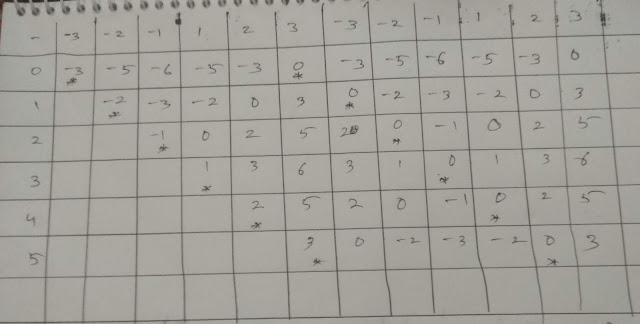
প্রব্লেম বুঝে থাকলে প্রথমে ১ টি টেবিল দেখে নেয়া যাকঃ
আমাদের কে একটি অ্যারে দেয়া আছে
ara[] = {-3 , -2 , -1 , 1 , 2 , 3}
- টেবিলের ১ম সারি হলো মূল অ্যারে (উল্লেখ্য অ্যারের সাইজ ৬। মূল অ্যারে টা কে ২বার রিপিট করা হয়েছে সলুশন এর সুবিধার্থে) ।
- ২য় সারি হলো মূল অ্যারের কিউমুলেটিভ সাম যা ০ সাইক্লিক শিফট এর জন্য কাজ করে। এই সারির ১ থেকে ৬ ইন্ডেক্স পর্যন্ত সাম অ্যারের ইলিমেন্ট গুলোর মধ্যে মিনিমাম টা ০ থেকে বড় হলে, ০ সাইক্লিক শিফট শর্ত মেনেছে এন্সার ১ বাড়ানো হবে।
- ৩য় সারি হলো ২য় ইলিমেন্ট থেকে বানানো কিউমুলেটিভ সাম। এই সারির ২ থেকে ৭ ইনডেক্স পর্যন্ত সাম অ্যারের ইলিমেন্ট গুলোর মধ্যে মিনিমাম টা ০ থেকে বড় হলে, ১ সাইক্লিক শিফট শর্ত মেনেছে। এন্সার ১ বাড়ানো হবে। (উল্লেখ্য এই সারিতে ১ নম্বর ইনডেক্স এর ঘর খালি রাখা হয়েছে)।
- এভাবে ৬ সাইজের একটা অ্যারের জন্য ০ থেকে ৫ পর্যন্ত সাইক্লিক শিফট বের করে কয়টা সাইক্লিক শিফট এর মিনিমাম ভ্যালু ০ থেকে বড় সেটাই এই প্রব্লেমে বের করতে বলা হয়েছে।
এখন, এভাবে প্রত্যেক সাইক্লিক শিফট এর জন্য সাম জেনারেট করা আমাদের জন্য সম্ভব নয়। আরো অপ্টিমাইজ কিছু বের করতে হবে। টেবিল এর দিকে তাকালেই বুঝতে পারবা যে,
- ০ সাইক্লিক শিফট এর জন্য সাম অ্যারে জেনারেট করলেই হয়।
- ০ সাইক্লিক শিফট এর সাম অ্যারের প্রত্যেক ইলিমেন্ট থেকে Sum[1] বিয়োগ করলে ১ সাইক্লিক শিফট এর সাম অ্যারে পাওয়া যায়।
- ০ সাইক্লিক শিফট এর সাম অ্যারের প্রত্যেক ইলিমেন্ট থেকে Sum[2] বিয়োগ করলে ২ সাইক্লিক শিফট পাওয়া যায়।
- তার মানে , ০ সাইক্লিক শিফট এর সাম অ্যারের প্রত্যেক ইলিমেন্ট থেকে Sum[i] বিয়োগ করলে iTh সাইক্লিক শিফট পাওয়া যায়।
এখন পর্যন্ত যা আলোচনা করেছি তা দিয়েও সলভ করা সম্ভব। প্রথমে সেগমেন্ট ট্রি বিল্ড করে প্রতি সাইক্লিক শিফট এর জন্য রেঞ্জ আপডেট, রেঞ্জ কুয়েরি চালিয়ে T*nlogn এ প্রব্লেম টা সলভ করা সম্ভব। ( এখনো কিছু জিনিস চিন্তা করতে হতে পারে!)
এবার আসা যাক T*n এ কিভাবে সলভ করা সম্ভব?
একচুয়েলি, প্রতিটা সাইক্লিক শিফট বের করার জন্য রেঞ্জ আপডেট চালানোর ই দরকার নেই।
০ সাইক্লিক শিফট বের করলেই সব কাজ করা সম্ভব।
- ০ সাইক্লিক শিফট এর সাম অ্যারের ১ থেকে ৬ ইনডেক্স এর মধ্যে মিনিমাম কত? -6 যা ০ সাইক্লিক শিফট এর জন্য মিনিমাম। এটি ০ থেকে ছোট হওয়ায় এই সাইক্লিক শিফট ভ্যালিড না।
- ০ সাইক্লিক শিফট এর সাম অ্যারের ২ থেকে ৭ ইনডেক্স এর মধ্যে মিনিমাম কত? -6 , এর থেকে Sum[1] = -3 বিয়োগ করলে থাকে -3 যা ১ সাইক্লিক শিফট এর সাম অ্যারের মিনিমাম। কিন্তু তা ০ এর ছোট হওয়ায় ভ্যালিড না।
- ০ সাইক্লিক শিফট এর সাম অ্যারের ৩ থেকে ৮ ইনডেক্স এর মধ্যে মিনিমাম কত? -6 এর থেকে Sum[2] = -5 বিয়োগ করলে থাকে -1 যা ২ সাইক্লিক শিফট এর সাম অ্যারের মিনিমাম। কিন্তু তা ০ এর ছোট হওয়ায় ভ্যালিড না।
- ০ সাইক্লিক শিফট এর সাম অ্যারের ৪ থেকে ৯ ইনডেক্স এর মধ্যে মিনিমাম কত? -6 এর থেকে Sum[3] = -6 বিয়োগ করলে থাকে 0 যা ৩ সাইক্লিক শিফট এর সাম অ্যারের মিনিমাম। এবং এটি ভ্যালিড কারণ তা ০ এর সমান অথবা বড় ।
এভাবে, শুধু ০ সাইক্লিক শিফট এর সাম অ্যারের নির্দিষ্ট ইনটারভাল এর মিনিমাম ভ্যালু বের করতে পারলেই প্রত্যেক সাইক্লিক শিফট ভ্যালিড কি না তা যাচাই করা যায়! আর মিনিমাম বের করার এই কাজ করা যায় n কমপ্লেক্সিটি তে স্লাইডিং রেঞ্জ মিনিমাম কুয়েরী ব্যাবহার করে!
বিঃদ্রঃ এই ব্লগ পড়ার পরও আরো কয়েকটা ইনপুট এর জন্য আউটপুট কিভাবে আসবে তা খাতা কলমে দেখার জন্য সাজেস্ট করা হচ্ছে।
Sliding Range Minimum Query সম্পর্কে জানতে ক্লিক করুন
Segment Tree সম্পর্কে জানতে ক্লিক করুন
Comments
Post a Comment