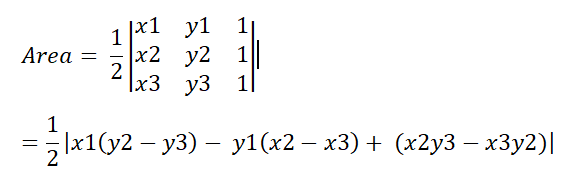Bappy's Blog

Problem Description  here প্রব্লেমঃ প্রব্লেমটিতে মূলত বলা হয়েছে, n সাইজের একটি অ্যারে a দেয়া থাকবে যেখানে n<=2e5 এবং a[i]<=1e6. অ্যারের All Possible Pair এর LCM এর যোগফল বের করতে বলা হয়েছে।  এই প্রব্লেমটি সলভ করার জন্য  Prerequisite-1  এবং  Prerequisite-2  দুইটি পর্ব অবশ্যই পড়তে হবে।  সল্যুশন আইডিয়াঃ ১) আমরা জানি, LCM(ai , aj) = (ai * aj) / GCD(ai , aj) । এখন, g GCD সম্বলিত কয়েকটি পেয়ার যদি (x1 , y1) , (x2 , y2) , (x3 , y3) হয় তবে পেয়ারগুলোর LCM এর যোগফল কী হবে? LCMSUM = ( (x1*y1) + (x2*y2) + (x3*y3) ) / g ২) এখন, একটি অ্যারে pairsum নিবো। pairsum[i] এর মধ্যে প্রাথমিকভাবে এমন সব পেয়ার এর গুণফলের যোগফল থাকবে যাদের GCD i অথবা i এর মাল্টিপল।  ৩) এখন, একটি অ্যারে a[] = {1 , 2 , 3 , 4 , 6 , 12} হলে, GCD 2 অথবা এর মাল্টিপল হবে কাদের? {2 , 4 , 6 , 12} এই সেট এর পেয়ারগুলোর। All possible pairsum = (2*4) + (2*6) + (2*12) + (4*6) + (4*12) + (6*12) এটিকে কীভাবে লিখা যায়? ( ( (2+4+6+12) * (2+4+6+12)) - (2^2 + 4^2 + 6^2 + 12^2) )/2 মানে সেট টি {x1 , x2 ,...

Problem Description  here প্রবলেমঃ প্রবলেমটিতে মূলত বলা হয়েছে, n সংখ্যক নোডের একটি ট্রি দেয়া থাকবে। সর্বনিম্ন কতগুলো নোড বাদ দিলে ট্রি এর ডায়ামিটার সর্বোচ্চ k হবে।  একটি ট্রি এর ডায়ামিটার বলতে বুঝানো হয় ট্রি এর যেকোন দুইটি নোডের মধ্যবর্তী দূরত্বগুলোর সর্বোচ্চ মান।  সল্যুশন আইডিয়াঃ  ১) প্রতিটি ডায়ামিটার এর একটা সেন্টার থাকে। সেন্টার থেকে দুইদিকের দূরত্ব সমান হয়।  ২) ডায়ামিটার এর দৈর্ঘ্য জোড় হলে সেন্টার হবে একটা নোড। আর বিজোড় হলে সেন্টার হবে একটা এজ।  ৩) এখন, ট্রি এর প্রতিটি নোড অথবা এজকে (k এর মান এর উপর নির্ভর করে) ডায়ামিটার এর সেন্টার ধরে দেখবো এই নোড বা এজ সেন্টার হলে কতগুলো নোড রাখা যায় অথবা কতগুলো নোড বাদ দিতে হয়? এভাবে, প্রতিটি নোড হিসেব করে সর্বনিম্ন কয়টা বাদ দেয়া যায় সেটা বের করা সম্ভব। 

সমস্যাঃ n(<=1e5) সাইজের একটি অ্যারে দেয়া থাকবে যেখানে a[i]<=1e5। ঐ অ্যারের যতগুলো পেয়ার সম্ভব তাদের GCD এর যোগফল বের করতে হবে।  এই প্রব্লেমটি পূর্বে আলোচিত  এই প্রব্লেম  এর উপর পুরোপুরি নির্ভরশীল।  আইডিয়াঃ আমি যদি 1 থেকে 10^5 পর্যন্ত প্রতিটি সংখ্যা x কয়টি পেয়ার এর GCD হওয়া সম্ভব সেটা রেফারেন্সের প্রব্লেম দ্বারা বের করতে পারি তাহলে প্রতিটি সংখ্যা x এর জন্য, sum += (x * number of pair those GCD equal to x)

সমস্যাঃ n(<=1e5) সাইজের একটি অ্যারে a দেয়া থাকবে যেখানে a[i] <= 1e5 এবং Q(<=1e5) টি কুয়েরী থাকবে। প্রতি কুয়েরী তে একটি সংখ্যা g দেয়া থাকবে। বলতে হবে অ্যারে তে এমন কয়টি সাবসেট আছে যাদের GCD = g.  বিঃদ্রঃ এই প্রব্লেমটি পূর্বে আলোচিত  এই প্রব্লেম  এর অনুরূপ একটি প্রব্লেম। আইডিয়াঃ ১) প্রথমত, আমরা চেষ্টা করবো এমন কয়টি সাবসেট বানানো সম্ভব যাদের GCD g অথবা এর মাল্টিপল। এই কাজটি আমরা কিভাবে করতে পারি?  1 থেকে 10^5 পর্যন্ত সবার ফ্রিকুয়েন্সী কাউন্ট করে রাখবো। এরপর, প্রতিটি সংখ্যার জন্য তার সম্ভাব্য সকল মাল্টিপল এর ফ্রিকুয়েন্সি যোগ করে পাবো এমন কয়টি সংখ্যা আছে যা ঐ সংখ্যা দ্বারা ভাগ করা যায়।  এখন, x দ্বারা বিভাজ্য এমন মোট অ্যারে এলিমেন্ট y হলে, yC1 + yC2 + yC3 + ---- + yCy = (2^y)-1  টি সাবসেট সম্ভব যাদের GCD g অথবা এর মাল্টিপল। ২) এখন, প্রতিটি সংখ্যা x এর জন্য এক্সেক্ট কতোগুলো সাবসেট আছে যাদের GCD = g? আমি যদি বের করতে পারি x এর প্রতিটি মাল্টিপল এর জন্য এক্সেক্ট সাবসেট কতোটি আছে তাহলে x এর জন্যও বের করতে পারি। বুঝতেই পারতেছো এই কাজটি বড় থেকে ছোট অর্ডারে করতে...

Problem:   n(<=1e5)  সাইজের একটি অ্যারে a দেয়া থাকবে যেখানে a[i]<=1e5 এবং q(<=1e5) টি কুয়েরী থাকবে। প্রতি কুয়েরী তে একটি সংখ্যা g দেয়া হবে। বলতে হবে অ্যারে তে এমন কয়টি পেয়ার (i,j) আছে যাদের GCD(a[i] , a[j]) = g এবং i<j আইডিয়াঃ ১) প্রথমত, আমরা চেষ্টা করবো এমন কয়টা পেয়ার সম্ভব যাদের GCD g অথবা এর মাল্টিপল। এই কাজটি আমরা কিভাবে করতে পারি?  ১ থেকে ১০^৫ পর্যন্ত সবার ফ্রিকুয়েন্সি কাউন্ট করে রাখবো। এরপর, প্রতিটি সংখ্যার জন্য তার সম্ভাব্য সকল মাল্টিপল এর ফ্রিকুয়েন্সি যোগ করে পাবো এমন কয়টি সংখ্যা আছে যা ঐ সংখ্যা দ্বারা ভাগ যায়।  এখন, x দ্বারা বিভাজ্য এমন মোট অ্যারে এলিমেন্ট y হলে, y C 2 বা (y*(y-1))/2 টি পেয়ার আছে যাদের GCD x অথবা তার মাল্টিপল।  ২) এখন, প্রতিটি সংখ্যা x এর জন্য এক্সেক্ট কতোগুলো পেয়ার আছে যাদের GCD = x এই কাজটি সহজেই করা যাবে। 

Problem:   (A * B)%M এর ভ্যালু কত সেটা বের করতে হবে যেখানে A<=1e18 , B<=1e18 , M<=1e18 Solution:  খুব ভালোভাবে বোঝা যাচ্ছে যে, ওভারফ্লো ই এই সমস্যার মূল সমস্যা -_- এখন, একটু ভিন্নভাবে চিন্তা করি প্রব্লেমটাকে।  x + x + x + x + x = 5x ৫ টা x যোগ করে পাওয়া যোগফল আর x এর সাথে ৫ গুণ করে পাওয়া গুণফল সমান। এটিই এই সমস্যা সমাধানের মূল কনসেপ্ট!  তার মানে, A*B হচ্ছে,  B সংখ্যাক A এর যোগফল। এখনো মাথায় না ঢুকলে কোড দেখতে পারোঃ

1. Intersection Of Two Segment: একমাত্রিক তলে দুইটি সেগমেন্ট (l1 , r1) এবং (l2 , r2) হলে, Segment-1:     ------------- Segment-2:               --------------- Intersect:                 ------- l = max(l1 , l2) r = min(r1 , r2) (l > r) হলে, Intersection   = 0 অন্যথায়, Intersection       = [l , r] 2. Intersection Of Two Rectangle: দ্বিমাত্রিক তলে অবস্থিত দুইটি আয়তের Upper Left Corner এবং Lower Right Corner এর স্থানাঙ্ক দেয়া থাকলে তাদের Intersection Area অথবা তাদের মধ্যকার কমন আয়তের জন্য বিন্ধু দুটি বের করতে হবে।  ১ম আয়তের বিন্ধু দুটি (x11 , y11) এবং (x12 , y12) ২য় আয়তের বিন্ধু দুটি (x21 , y21) এবং (x22 , y22) Intersect করা অংশটিকে আয়ত ধরলে সেই আয়তের বিন্ধু দুটি হবে, (x31 = max(x11 , x21) , y31 = min(y11 , y21)) এবং (x32 = min(x12 , x22) , y32 = max(y12 , y22)) IF(x31 > x32 || y31>y32)     No Intersection else     [(x31,y31) - (x32...

Problem Description  here প্রব্লেমটিতে মূলত বলা হয়েছে, একটা ডিকশনারি দেয়া থাকবে যেখানে n টি শব্দ থাকবে। প্রতিটি শব্দের ১ম এবং শেষ ক্যারেক্টার ছাড়া বাকি ক্যারেক্টার গুলো যেভাবে ইচ্ছা সাজানো যায়। এরপর একটি বাক্য দেয়া থাকবে। এই বাক্যের শব্দগুলোও একইভাবে সাজানো যায়। বলতে হবে ডিকশনারি থেকে শব্দ নিয়ে ব্যাকটি কতভাবে গঠন করা যায়?  সলুশ্যন আইডিয়াঃ ১) প্রতিটি শব্দ ডিকশনারী তথা ট্রাই তে ইনসার্ট করার সময়ই ঐ শব্দের ২য় থেকে সর্বশেষ ক্যারেক্টার এর আগ পর্যন্ত সর্ট করে নিবো লেক্সিকোগ্রাফিক্যালি। এবং ট্রাই তে প্রতিটি নোডে কতটা স্ট্রিং শেষ হয়েছে সেটা ক্যালকুলেট করে রাখবো।  ২) এরপর, বাক্যের প্রতিটি শব্দও একইভাবে সর্ট করবো এবং দেখবো ডিকশনারী তে এই শব্দটি কতবার ইনসার্ট আছে। প্রতিটি শব্দের ফ্রিকুয়েন্সী গুণ করে গুণফলই হবে এন্সার।  এখন, প্রব্লেমটি তোমার নিজে নিজে সলভ করার চেষ্টা করা উচিৎ। এরপরও না পারলে নিজ দায়িত্বে সলুশ্যন দেখতে পারো। বিঃদ্রঃ সলুশ্যন দেখে প্রব্লেম সলভ করা ভালো প্র্যাকটিস না। 

Problem Description  here প্রব্লেমটিতে মূলত n সাইজের দুইটি স্ট্রিং দেয়া থাকবে। দুইটি স্ট্রিং এর মধ্যকার Longest Common Substring টি প্রিন্ট করতে হবে।  সলুশ্যন আইডিয়াঃ  ১) বাইনারী সার্চ করে আমরা সর্বোচ্চ কোন Length এর কমন সাবস্ট্রিং সম্ভব বের করে নিবো।  ২) নির্দিষ্ট Length এর কমন সাবস্ট্রিং সম্ভব কি না এই কাজটি কীভাবে করবো? শুরুতে দুইটা স্ট্রিং এর জন্য Prefix Hash বের করে রাখবো। এরপর, প্রথম স্ট্রিং এর জন্য এই নির্দিষ্ট সাইজের যতোগুলো সাবস্ট্রিং পসিবল তাদের হ্যাশ ভ্যালু ম্যাপে সেইভ রাখবো।  এখন, দ্বিতীয় স্ট্রিং এও যদি এই নির্দিষ্ট সাইজের সাবস্ট্রিং এর জন্য এমন একটি হ্যাশ ভ্যালু পাই যা অলরেডি ম্যাপে আছে তারমানে এই সাইজের কমন সাবস্ট্রিং বানানো সম্ভব।  এই প্রব্লেমে সেটার এমন কিছু টেস্টকেস দিয়েছে যে সিংগেল হ্যাশিং এর ক্ষেত্রে কলিশন হওয়ার সম্ভাবনা অনেক বেশি। এজন্য, ডাবল হ্যাশিং করাই শ্রেয়।  এখন প্রব্লেমটি তোমার নিজে নিজে সলভ এর চেষ্টা করা উচিৎ। এরপরেও না পারলে নিজ দায়িত্বে সলুশ্যন দেখতে পারো। বিঃদ্রঃ সলুশ্যন দেখে প্রব্লেম সলভ ভালো প্র্যাকটিস না।

Problem Description  here সহজ ভাষায় বলতে গেলে, একটা অ্যারে দেয়া থাকবে। এই অ্যারে থেকে এমন একটা সাবঅ্যারে সিলেক্ট করতে হবে যাতে এই সাবঅ্যারের সব সংখ্যাগুলোর XOR সর্বোচ্চ হয়। একইভাবে, এমন একটা সাবঅ্যারে সিলেক্ট করতে হবে যাতে এই সাবঅ্যারের সংখ্যাগুলোর XOR সর্বনিম্ন হয়। সর্বোচ্চ এবং সর্বনিম্ন সংখ্যাটি প্রিন্ট করতে হবে।  সলুশ্যন আইডিয়াঃ সাবঅ্যারের XOR কথাটি আসলেই মূলত  PrefixXOR এর আইডিয়া আসে।  ১) অ্যারেটির PrefixXOR বের করে রাখবো। এখন, অ্যারের l to r ইনডেক্সের XOR মানে কী?  PrefixXOR[r] ^ PrefixXOR[l-1] ২) ক্রমানুসারে প্রতিটি PrefixXOR এর বিট গুলো নিবো MSB থেকে LSB। আমি যদি এখন PrefixXOR অ্যারের ith পজিশনে থাকি তাহলে ট্রাই তে 0 to (i-1) পজিশন পর্যন্ত PrefixXOR অ্যারের প্রতিটা এলিমেন্ট এর বিট সিকুয়েন্স স্টোর করা আছে।  এখন, বর্তমান এলিমেন্ট এর জন্য এর পূর্বের অল পসিবল সাবঅ্যারের XOR এর কাজটা আমরা ট্রাই তে স্টোরড ডেটা থেকে করতে পারি। কীভাবে? বর্তমান বিট সিকুয়েন্স এর একটা পজিশনে যদি ০ থাকে আমি চেষ্টা করবো ট্রাই এর বর্তমান নোড থেকে ১ এর পথে যেতে। বিট সিকুয়েন্সে যদি...

Prefix Sum: মনে কর, তোমাকে একটা অ্যারে দেয়া আছে 10^5 সাইজের। এবং 10^5 সংখ্যক কুয়েরী দেয়া থাকবে। প্রতি কুয়েরী তে left এবং right দুইটা ভ্যারিয়েবল দেয়া থাকবে। বলতে হবে,  ara[lft] + ara[lft+1] + --- + ara[rgt-1] + ara[rgt] = কত? মানে, left থেকে right তম ইনডেক্স পর্যন্ত সাবঅ্যারে টার যোগফল কত?  এই কাজটিই আমরা Prefix Sum দ্বারা করতে পারি। যেখানে, PrefixSum[i] =  1 থেকে i তম ইনডেক্স পর্যন্ত অ্যারের এলিমেন্টগুলোর যোগফল। তাহলে, আমরা লিখতে পারি, PrefixSum[i] = PrefixSum[i-1] + ara[i] Sum[l...r] = PrefixSum[r] - PrefixSum[l-1] Prefix XOR: Prefix XOR টার্মটাও মোটামুটি Prefix Sum এর অনুরূপ। এই প্রব্লেমে আমাকে বার বার কুয়েরী করা হবে left থেকে শুরু করে right পর্যন্ত অ্যারের সংখ্যাগুলোর XOR কত?  এই কাজটি আমরা করবো Prefix XOR দিয়ে। যেখানে, PrefixXOR[i] = 1 থেকে i তম ইনডেক্স পর্যন্ত অ্যারের এলিমেন্টগুলোর XOR। তাহলে, PrefixXOR[i] = PrefixXOR[i-1] ^ ara[i] XOR[l...r] = PrefixXOR[r] ^ PrefixXOR[l-1]

একটি ত্রিভুজের শীর্ষত্রয়  A,B,C  এবং অপর একটি বিন্ধু D এর স্থানাঙ্ক দেয়া আছে বের করতে হবে  D  বিন্ধু ত্রিভুজের অভ্যন্তরে অবস্থিত কি না। আইডিয়া-১ঃ  যদি, ত্রিভুজ ক্ষেত্র ABC = ত্রিভুজ  ক্ষেত্র   ABD + ত্রিভুজ  ক্ষেত্র   ADC + ত্রিভুজ  ক্ষেত্র   BCD হয় তবে D বিন্ধু ত্রিভুজ ABC এর অভ্যন্তরে অবস্থিত।     আইডিয়া-২ঃ   A,B,C,D  বিন্ধুদ্বয়ের জন্য  Convex Hull  তৈরী করলে  Convex Hull  এর প্রান্ত বিন্ধু যদি ৩ টি হয় তবে  D  বিন্ধু ত্রিভুজের অভ্যন্তরে অবস্থিত।  যদি প্রান্তবিন্দু ৪ টি হয় তবে তা ত্রিভুজের বাইরে অবস্থিত। আইডিয়া-৩ঃ   D  বিন্ধু যদি  AB,BC,CA  বাহুত্রয়ের বামে অবস্থিত হয় তার মানে এটি ত্রিভুজের অভ্যন্তরে অবস্থিত।

             একটি ত্রিভুজের শীর্ষত্রয়ের স্থানাঙ্ক দেয়া থাকলে ত্রিভুজটির ক্ষেত্রফল নির্ণয়ঃ বিন্ধুত্রয় A(x1,y1) , B(x2,y2) , C(x3,y3) হলে,

          তিনটি বিন্দুর স্থানাঙ্ক A(x1,y2) , B(x2,y2) , C(x3,y3). C বিন্দুটি AB রেখার বামে, ডানে নাকি      AB বরাবর অবস্থিত?   আইডিয়াঃ  ABC ত্রিভুজের  ক্ষেত্রফল যদি ধনাত্মক হয়(মডুলাস ব্যাবহার না করে) তবে C বিন্ধু AB রেখার বামে অবস্থিত। ক্ষেত্রফল ঋণাত্মক হলে C বিন্ধু AB রেখার ডানে অবস্থিত। আর ক্ষেত্রফল ০ হলে বিন্দুত্রয় একই রেখায় অবস্থিত।

Problem Description  here প্রব্লেমটিতে বলা হয়েছে, একটি রেঞ্জ এর মধ্যে এমন কয়টি সংখ্যা আছে যাদের মধ্যে ৩,৬ এবং ৯ ডিজিটগুলো সমান সংখ্যকবার আছে এবং কমপক্ষে একবার করে আছে।  সল্যুশন আইডিয়াঃ এই প্রব্লেমের কিছু অবজার্বেশন আছে।  ১) সবচেয়ে বড় সংখ্যাটি (১০^৫০) তে সর্বোচ্চ ৫১ টি ডিজিট থাকতে পারে। তার মানে, প্রব্লেমের শর্ত পূরণ করে এমন সংখ্যায় ৩,৬,৯ প্রতিটি ডিজিট সর্বোচ্চ ১৬বার থাকতে পারে। এর বেশি হলে সেই সংখ্যাটি আমাদের প্রয়োজন নেই। এতোটুকু বুঝতে পারলে আর ডিজিট ডিপি মোটামুটি পারলে হয়তো মনে মনে কিছু স্টেট ধরে নিয়েছো। তাদের মধ্যে তিনটি স্টেট হলো,  i) কয়টা ৩ পেলাম এখন পর্যন্ত। ii) কয়টা ৬ পেলাম এখন পর্যন্ত। iii) কয়টা ৯ পেলাম এখন পর্যন্ত। এই তিনটা স্টেট এর জন্য কমপ্লেক্সিটি ১৭*১৭*১৭ = ৪৯১৩ এবার, প্রব্লেমটি ইমপ্লিমেন্ট করলে তোমার TLE খাওয়ার সম্ভাবনা প্রবল!!!  আরো কিভাবে অপটিমাইজ করা যায় ভাবতে হবে। .......... .......... ভাবা শেষেও না পেলে দেখো। আমি যদি দুইটা স্টেট নেই যাদের কাজ হচ্ছে, ৩ ও ৬ এর সংখ্যার পার্থক্য রাখা। ৩ ও ৯ এর সংখ্যার পার্থক্য রাখা। তাহলে স্টেট দুটির কমপ্লেক্সিটি হ...

উপরের চিত্রের মতো বিদঘুটে কোন বহুভুজের ক্ষেত্রফল বের করতে ব্যাবহৃত হয় পিক'স থিওরি! যদি বহুভুজটির ভার্টেক্স বা কৌণিক বিন্ধুসমূহ গ্রাফ পেপারের ইন্টিজার পয়েন্টগুলো হয় তবে বহুভুজটির ক্ষেত্রফল হবেঃ Area = i + (b/2) - 1 = (2*i + b - 2)/2 এখানে,      i - Number of points inside the polygon                     b - Number of points on the boundary of the polygon এখন, পিক'স থিওরি টা আসলে যেভাবে আসছেঃ ১) আমি যদি গ্রাফ পেপারে লম্বভাবে অবস্থিত অথবা অনুভুমিকভাবে অবস্থিত ২ টি বিন্দুর মধ্যবর্তী দূরত্ব এক একক ধরি তবে গ্রাফ পেপারে অংকিত ক্ষুদ্রতম ত্রিভূজের ক্ষেত্রফল হবে ১/২।  (এখানে, ক্ষুদ্রতম ত্রিভুজ বলতে বুঝানো হয়েছে এমন একটা ত্রিভুজ যার কৌণিক বিন্ধুগুলো গ্রাফ পেপারের ইন্টিজার পয়েন্ট হবে কিন্তু ত্রিভুজের অভ্যন্তরে কোন ইন্টিজার পয়েন্ট থাকবে না।অর্থাৎ, যার b=3 , i=0 )। এমন সকল ত্রিভুজের ক্ষেত্রফল ই ১/২ হবে শতভাগ নিশ্চিত। ২) এবার আমি বহুভুজটিকে ক্ষুদ্রতম ত্রিভুজে স্প্লিট করবো। ৩) তাহলে, বহুভুজটির ক্ষেত্রফল বের করতে পারবো যদি ...

Problem Description  here এখন পর্যন্ত আমার সলভ করা ডিজিট ডিপির প্রব্লেমগুলোর মধ্যে অন্যতম মজার প্রব্লেম এই প্রব্লেমটি।  সংবিধিবদ্ধ সতর্কীকরণঃ এই পর্বের লিখা কিছুটা দীর্ঘায়িত হতে পারে। যা সম্পূর্ণ অনিচ্ছাকৃত । ডিজিট ডিপির ব্যাসিক আইডিয়া না জানলে এই পর্ব না পড়াই উত্তম। সেক্ষেত্রে, নিচের লিংক থেকে ব্যাসিক ডিজিট ডিপি শিখে আসা উচিৎ। Digit DP in English Digit DP in Bengali প্রব্লেমটিতে বলা হয়েছে, একটা রেঞ্জ এর মধ্যে যেসব সংখ্যা ৩ দ্বারা বিভাজ্য কিন্তু ৭ দ্বারা বিভাজ্য নয় এবং যাদের বাইনারী রিপ্রেজেন্টেশনে সর্বোচ্চ Maxone সংখ্যক 1 থাকতে পারে এবং একটি আইডিয়াল নাম্বার এর সাথে বিট ডিফারেন্স সর্বোচ্চ k হতে পারে তাদের যোগফল বের করতে।  ২য় টেস্টকেস টা যদি দেখিঃ 1 6 2 3 2 1 থেকে 6 পর্যন্ত সংখ্যাগুলোর বাইনারী রিপ্রেজেন্টেশন হচ্ছেঃ 1 - 00000000000000000000000000000001 2 - 00000000000000000000000000000010 3 - 00000000000000000000000000000011 4 - 00000000000000000000000000000100 5 - 00000000000000000000000000000101 6 - 00000000000000000000000000000110 আইডিয়াল নাম্বার ৩ এর বাইনারী হচ্ছেঃ 0000...